Should we use MRP
for simulating area-level outcomes?

– Roger Beecham
– Stephen Clark

Small area estimation

Start : SAE

Assume : no knowledge

Small area estimation

1. In social sciences, we often use samples from surveys to estimate the characteristics of a population.

Small area estimation

2. These samples are usually desgined to be representative nationally.

We think we can estimate smoking as a population parameter reasonably well from HSE.

Small area estimation
– direct estimation

3. If we have enough sample we we might be able to subset by Region - to sum up number of smokers in each. directly estimate a subnational population by subdividing

Small area estimation
– direct estimation

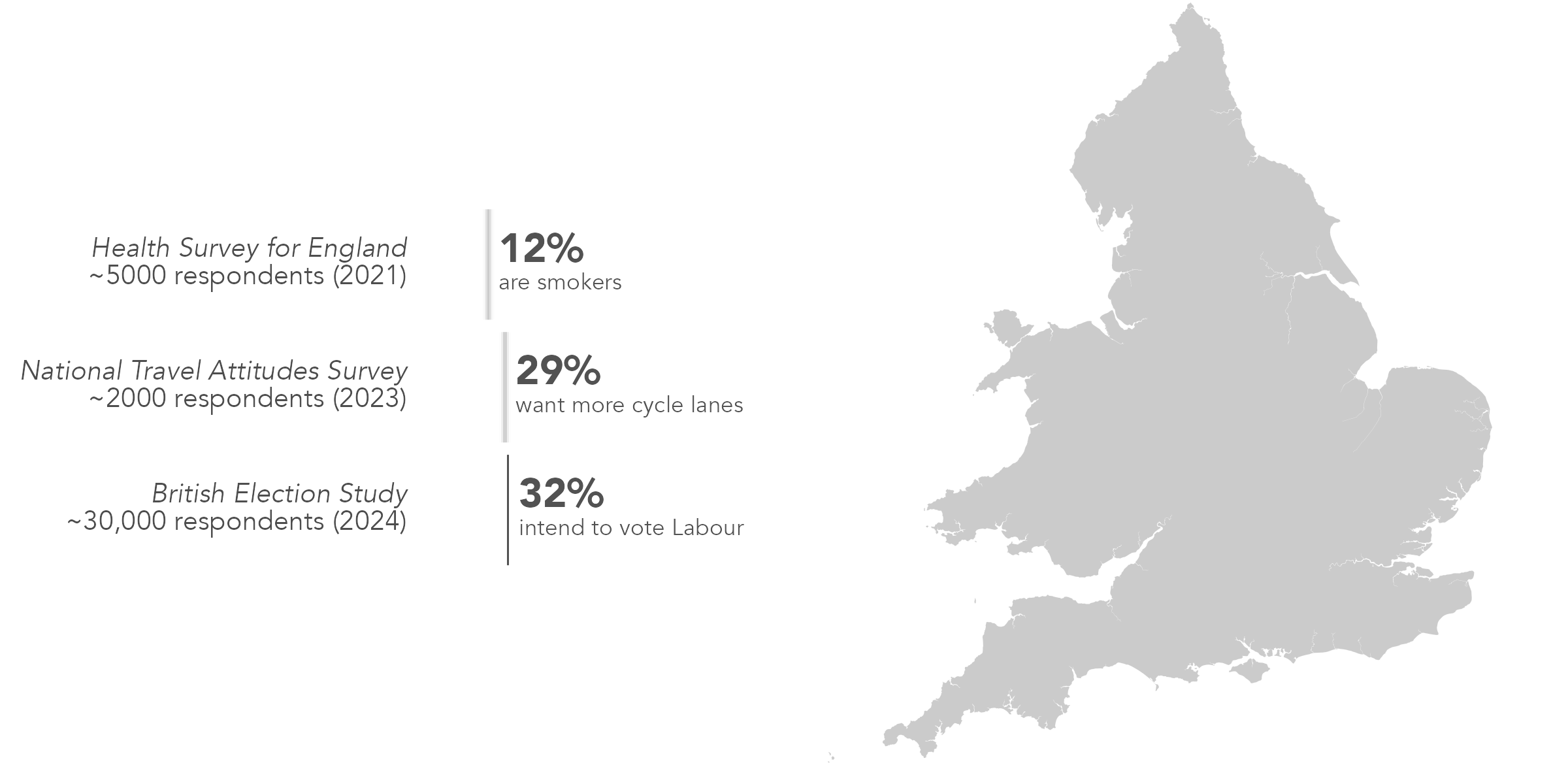
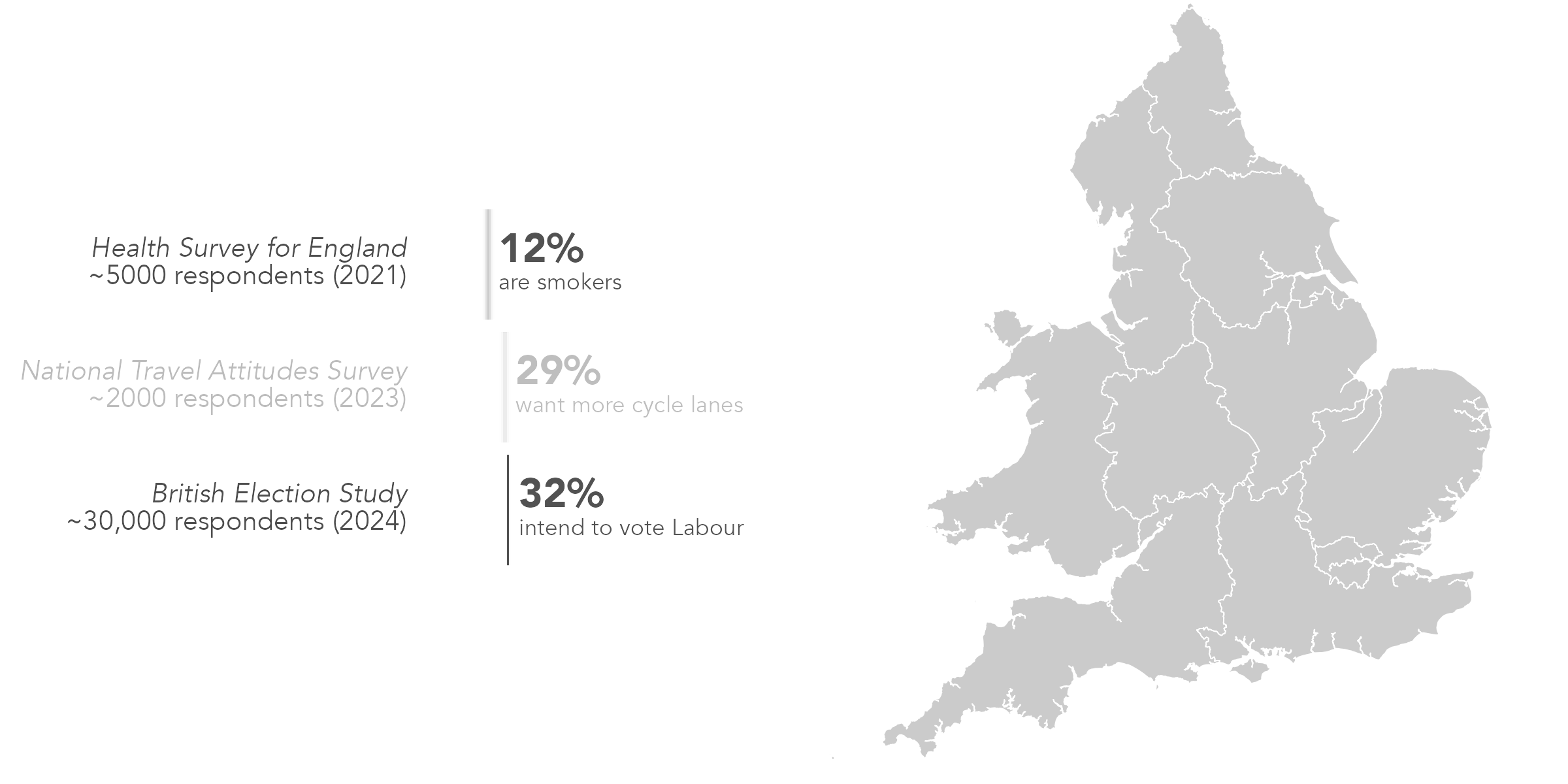
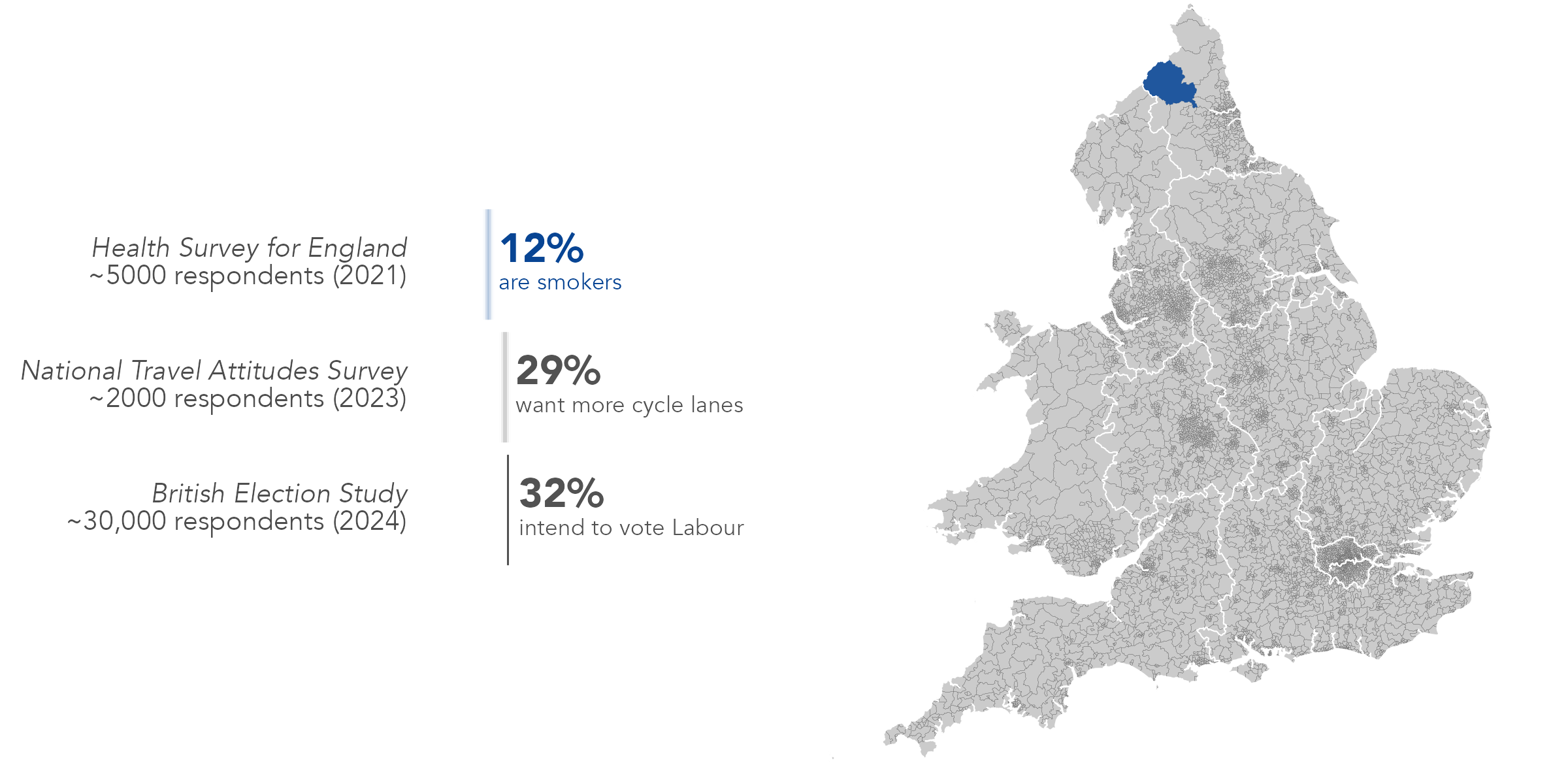
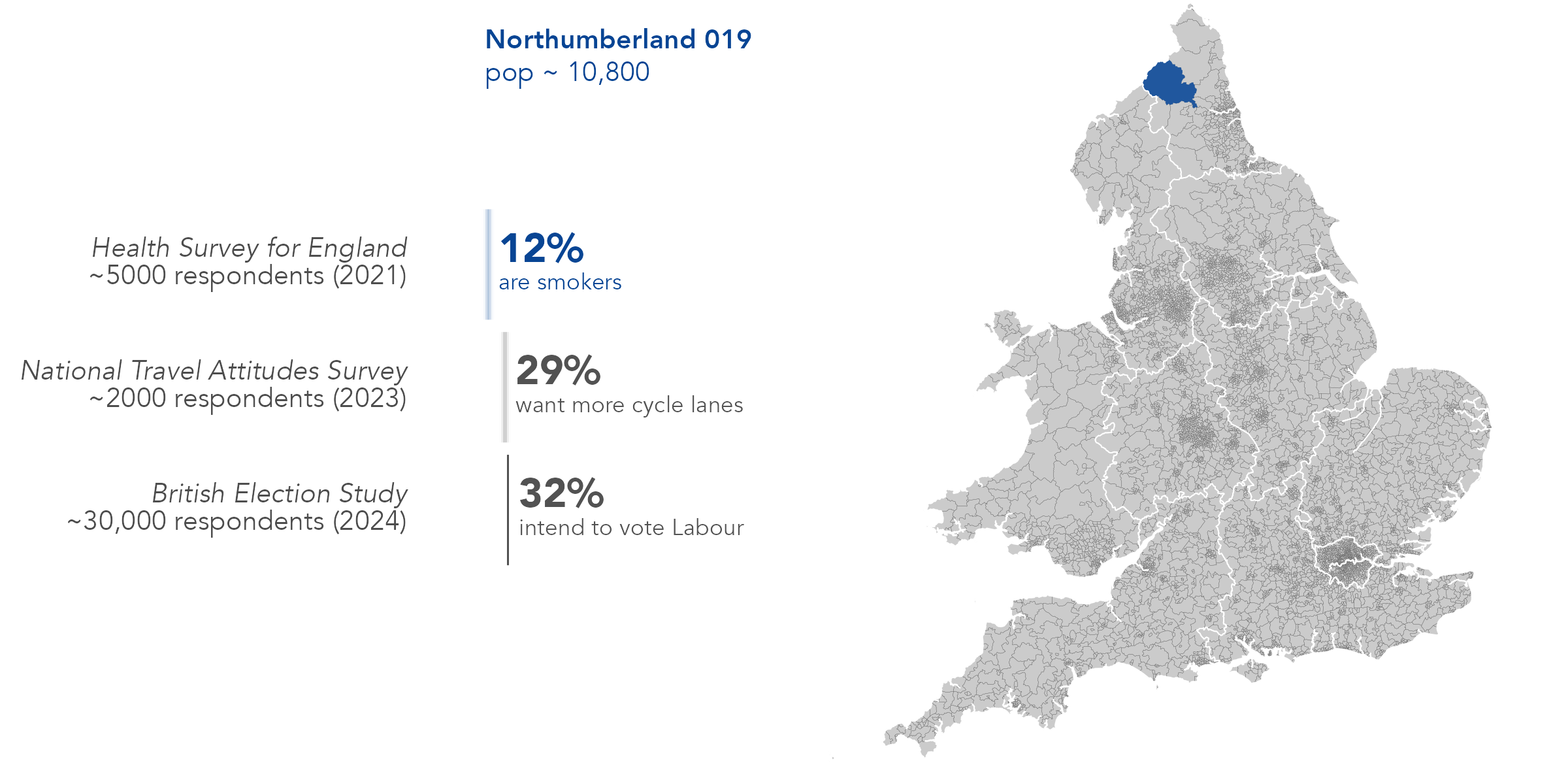
Small are estimation is where we use survey data to estimate an unknown outcome – smoking, beliefs about cycling, voting intention – for subpopulations (small areas) where sample sizes are too small for direct estimation.

4. But we can’t do direct estimation – subdividing – when looking at how an outcome is in smaller areas.

Spatial microsimulation

Spatial microsimulation

1. Start with survey of individuals and some small areas that we want to estimate our outcome over.
2. Allocate individuals to each small area sampling with replacement from individual survey data so that it sums to the total number living in that area.

Spatial microsimulation

3. So if this MSOA has 11k people, we’d sample from our survey that number of individuals – then count up on the target outcome.
4. Could do this sampling randomly.

Spatial microsimulation

But then we’d assume that our target outcome is uniformly distributed across small areas – that it doesn’t vary.

Spatial microsimulation

4. If we knew, either from some analysis on the survey dataset or existing knowledge, that our target outcome varies systematically by demographics or some other area-level context.

5. So if this area contained c.1400 women aged 50-64 we constrain our sample – make sure that the total counts of survey respondents we’re allocating approximates to the joint sums of that demographic in that area.

Spatial microsimulation assumptions

1. Survey data are sufficiently large and rich to be reproduce the diversity of individuals in a small area.

2. The target / outcome being simulated is associated with the constraint variables.

3. That this association is stable and geographically uniform.

Quite big assumptions

But of course this would only make sense if we think our outcome of interest at the area-level was cleanly associated with the demographic composition of those areas – and that area-level context was very unlikely to affect our target outcome.

3 Ideally outcome of interest is stable to geographic context –

if we thought that our we believed that each small area was composed of an entirely uniform mix of people, or had context that

Multilievel Regression w/ Poststratification

MRP the same goals – but model-based approach.

Andrew Gelman and Thomas Little (1997)
Poststratification into many categories using hierarchical logistic regression
Survey Methodology, 23(2): 127–135

Notoriety Political Opinion research: explaining polling missess 2016

use hierarchical regression to come up with estimates of public opinion across a wide range of demographic and geographic subgroups (poststratification cells) – even when survey sample sizes are small in many of those cells.

Show basic regresion formula

Basic MRP setup: a model estimating an outcome y based on set of variables x known in the population (these are constraints) – highlight R Fit a regression model of y on x and then averaging over the cells in proportion to their known population counts

Show basic regression formula predicting out. P

Update basic regression formula with multilevel. M

Desire to poststratify on as many factors as possible, and a regression model with a large number of predictors and interactions cannot be estimated stably using least squares.

A key attribute of MRP (or RRP) is that it allows predictions for y given values of x that are not observed in the sample, or which have such small counts in the sample that it would be impossible to make predictions for them from local data alone.

group-level predictors for multilevel regressions (so that, for example, inferences for small states in a national survey are partially pooled toward reasonable state-level estimates rather than to a national baseline); adjusting for non-census variables, in which case the population counts of the poststratification cells themselves must be estimated from the data

Andrew Gelman and Thomas Little (1997)
Poststratification into many categories using
hierarchical logistic regression
Survey Methodology, 23(2): 127–135

A key attribute of MRP is that it allows predictions of y [an outcome] given values of x [constraints] that are not observed in the sample, or which have such small counts in the sample that it would be impossible to make predictions for them from local data alone.

MRP workflow

MRP workflow

1. Estimate mutilevel model of the target outcome, using

   • individual-level demographic types (that are known in the Census)
   • area-level context variables
   • pooled estimates via random intercepts, ideally on small-areas being simulated

MRP workflow

1. Estimate mutilevel model of the target outcome, using

   • individual-level demographic types (that are known in the Census)
   • area-level context variables
   • pooled estimates via random intercepts, ideally on small-areas being simulated

2. Collect per small-area, the joint counts of individuals by demographic types ~ the poststratification frame.

3. Predict from the model for all demographic type and context combinations, by small-area.

4. Weight those predicted probabilities using the small-area joint counts (the poststratification frame) and add up the target outcome.

Our thesis
– for MRP over SPM

Our thesis

1. Since it uses multilevel model designs – pooled estimates – MRP can estimate outcomes in small-areas poorly represented by survey data.

2. MRP adjusts for things that should bother us as geographers: modelled outcomes can reflect geographic dependency in outcome and heterogeneity in process.

3. MRP invites us to think in a principled way about the outcome and our inferences – as we explicitly model that outcome.

Complex relationships and interactions: political polling age and education.

Comparison

Survey ~7,000 respondents

~Population

Target outcome

How is your health in general?
1. Very good
2. Good
3. Fair
4. Bad
5. Very Bad

Survey ~7,000 respondents

~Population

Target Known outcome

How is your health in general?
1. Very good
2. Good
3. Fair
4. Bad
5. Very Bad

Survey ~7,000 respondents

~Population

Target Known outcome

How is your health in general?
1. Very good
2. Good
3. Fair
4. Bad
5. Very Bad

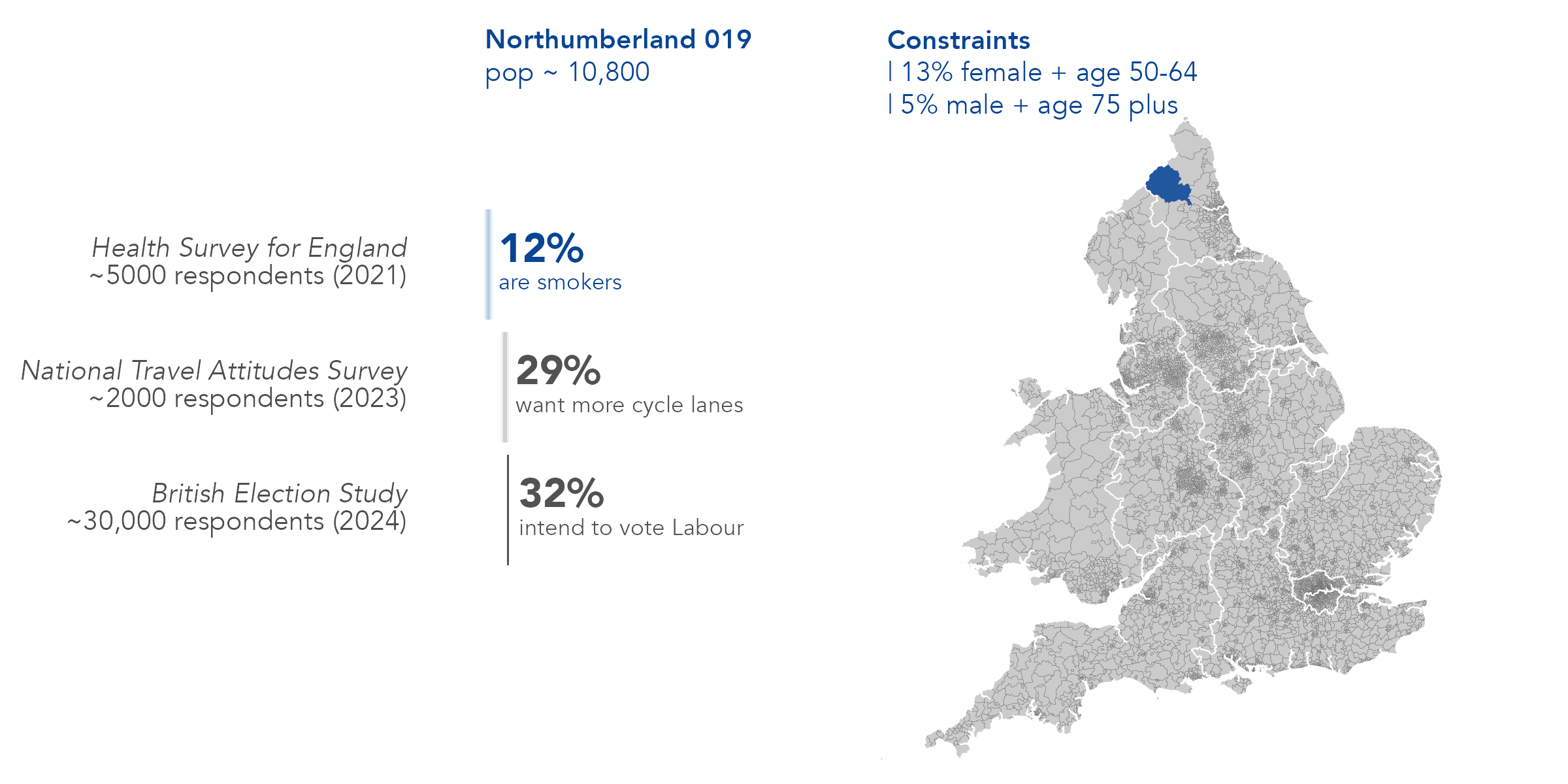
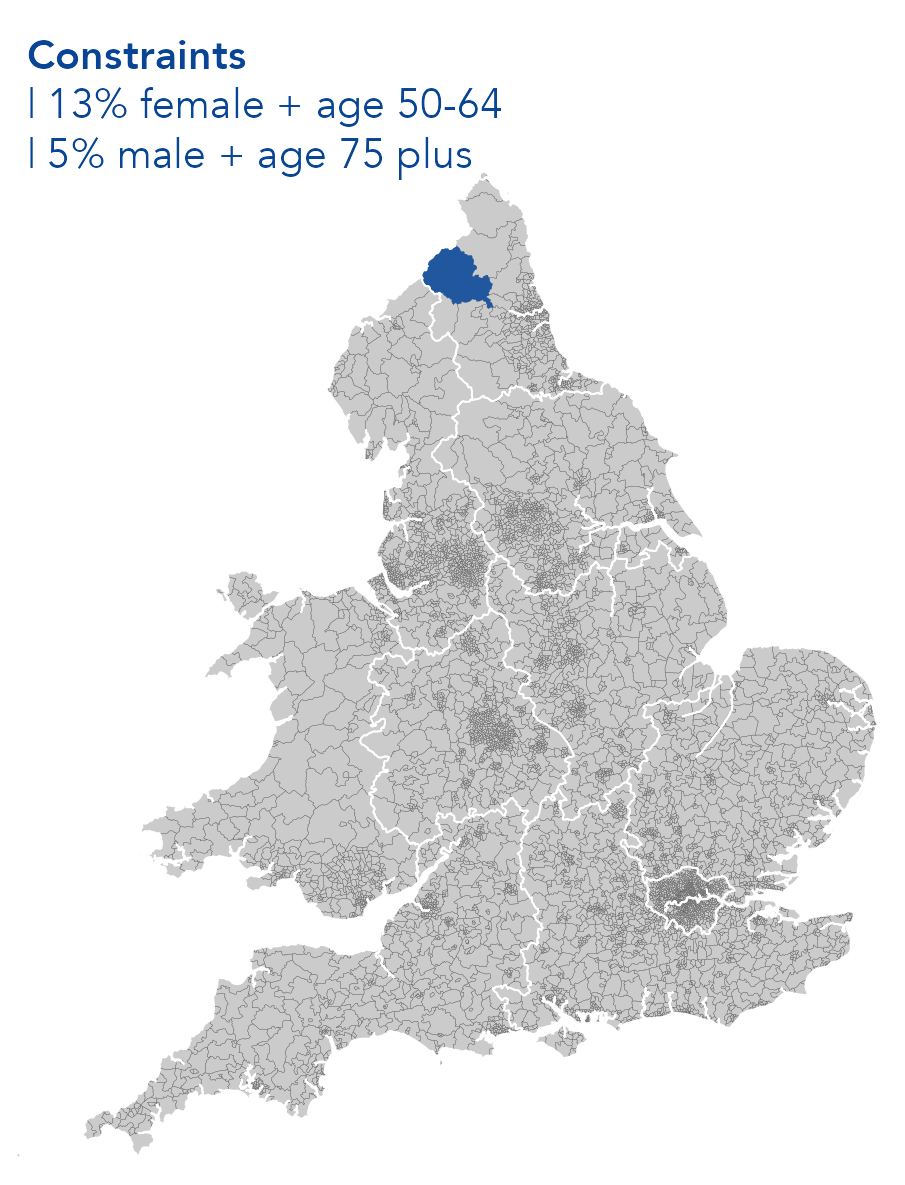
• demographic types
  • sex {F | M}
  • age {0-15 | 16-24 | 25-34 | 35-49 | 50-64 | 65+}
  • education {level0 | level1/2 | level3 | level4}
    

• area-level context
  • imd {1 most deprived | 2 | 3 | 4 | 5 least deprived}
  • region {EM | E | Ldn | NE | SE | SW | WM | Y&H}
  • rurality {urban | rural}

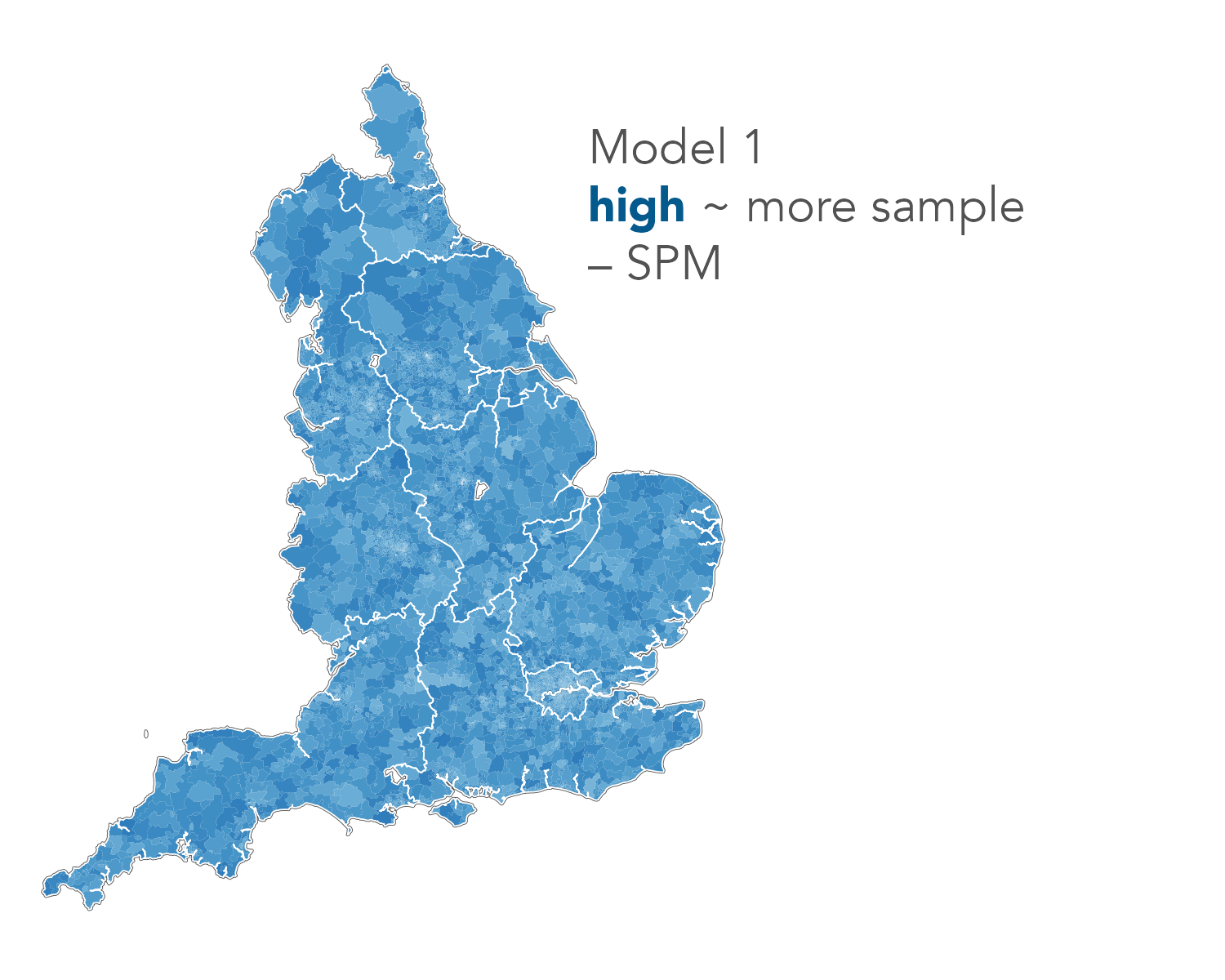
SPM designs

• Model 1
  • {sex + age}
• Model 2
  • {sex + age + imd}
• Model 3
  • {sex + age + urban-rural}
• Model 4
  • {sex + age + region}
• Model 5
  • {sex + age + region + imd}
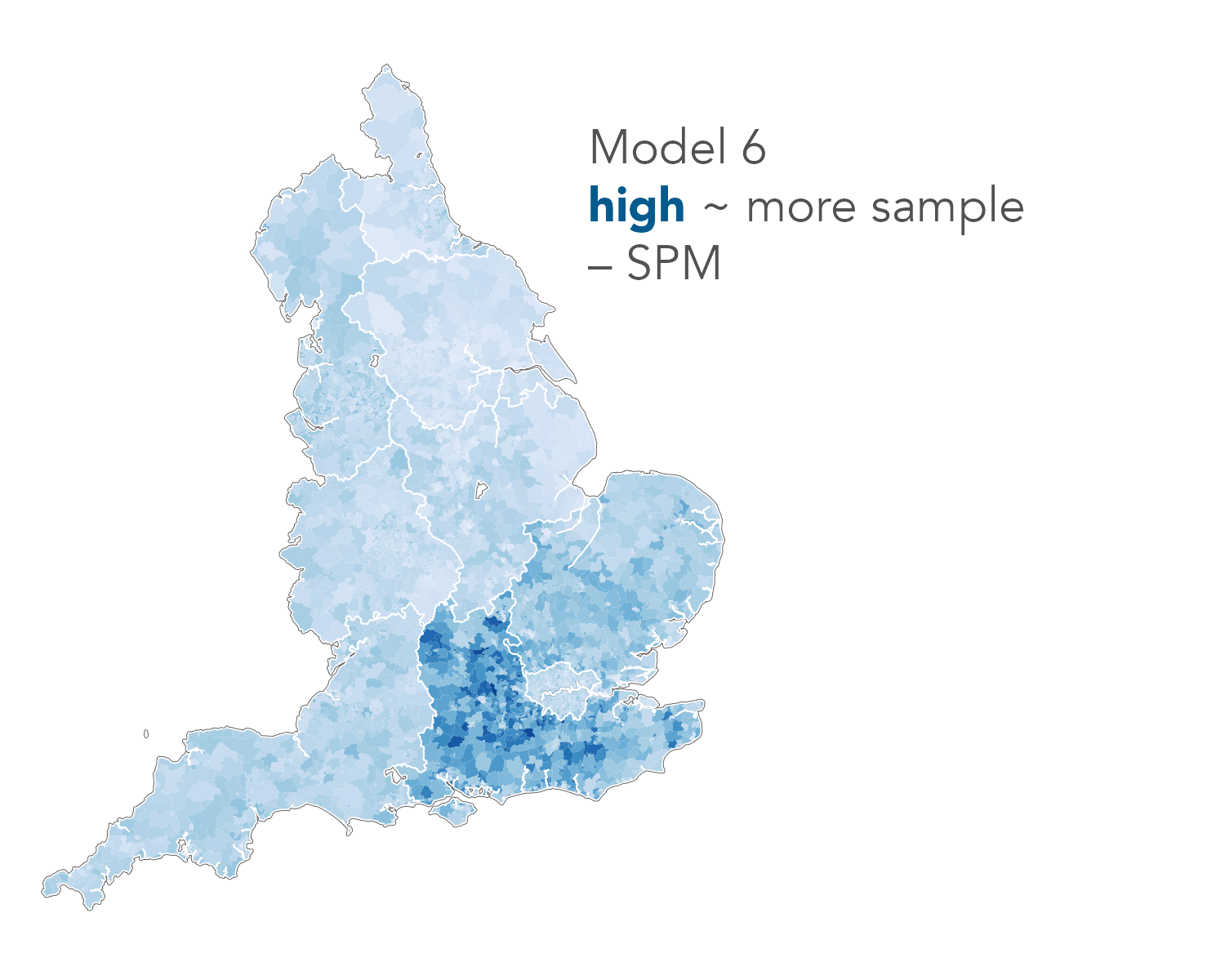
• Model 6
  • {sex + age + region + education}

MRP designs

• Model 1
  • {sex + age}
• Model 2
  • {sex + age + imd}
• Model 3
  • {sex + age + urban-rural}
• Model 4
  • {sex + age + region}
• Model 5
  • {sex + age + region + imd}
• Model 6
  • {sex + age + region + education}

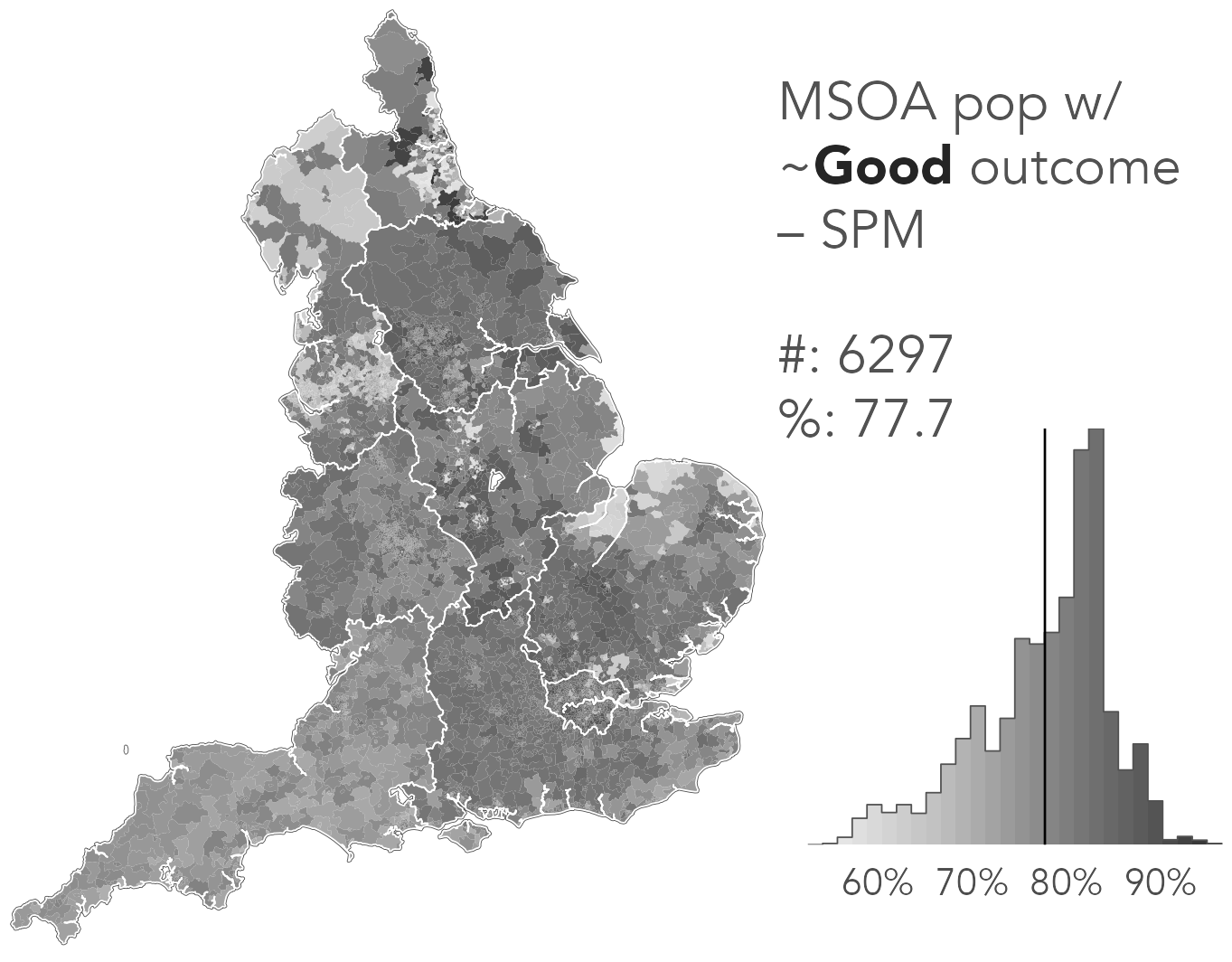
Comparison metrics

• Mean Absolute Error
  • # good | % good
• Pearson Residuals
  • obs-model / sqrt(model)
• Shannon Entropy
  • SPM only

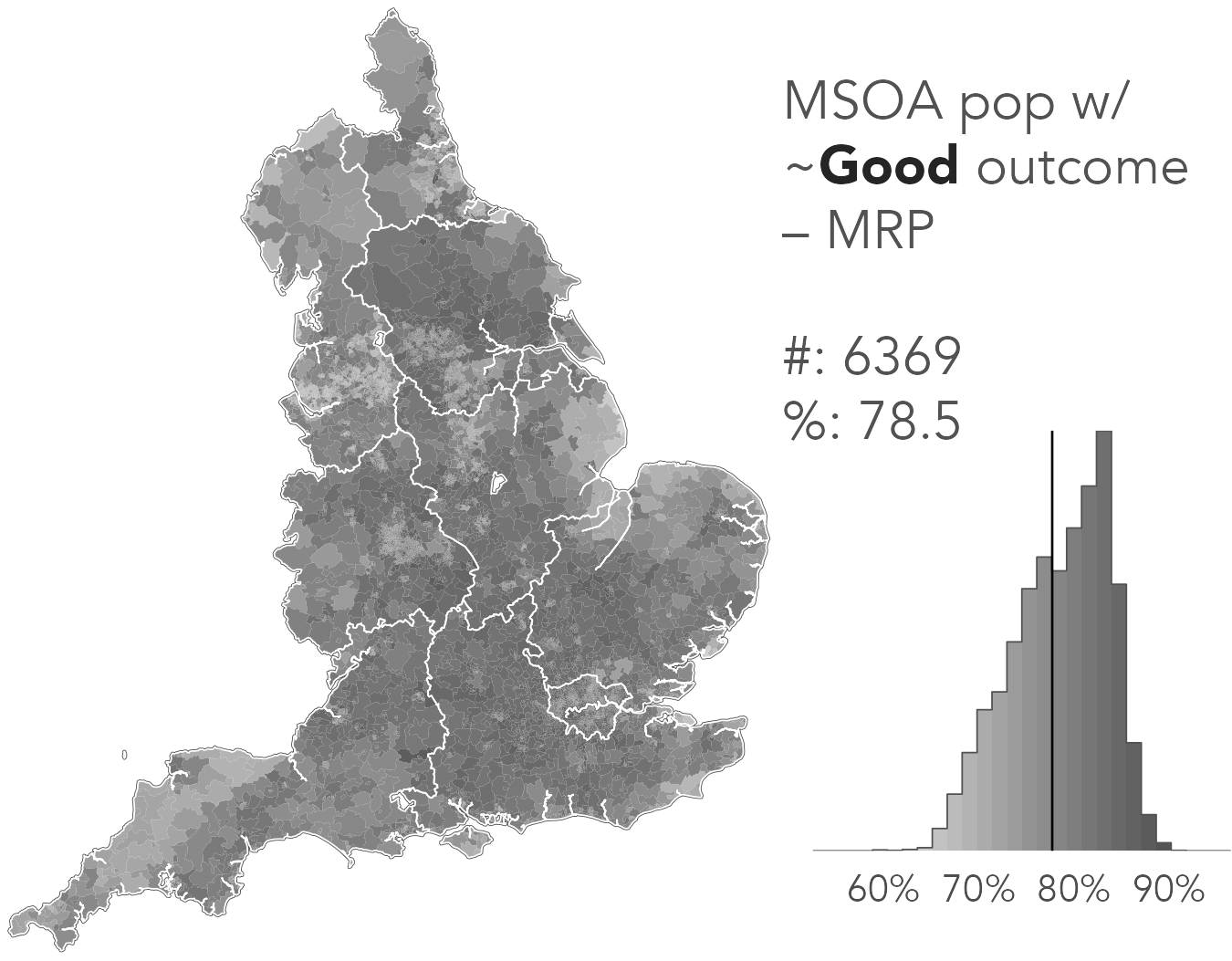
Comparison metrics

• Mean Absolute Error
  • # good | % good
• Pearson Residuals
  • obs-model / sqrt(model)
• Shannon Entropy
  • SPM only

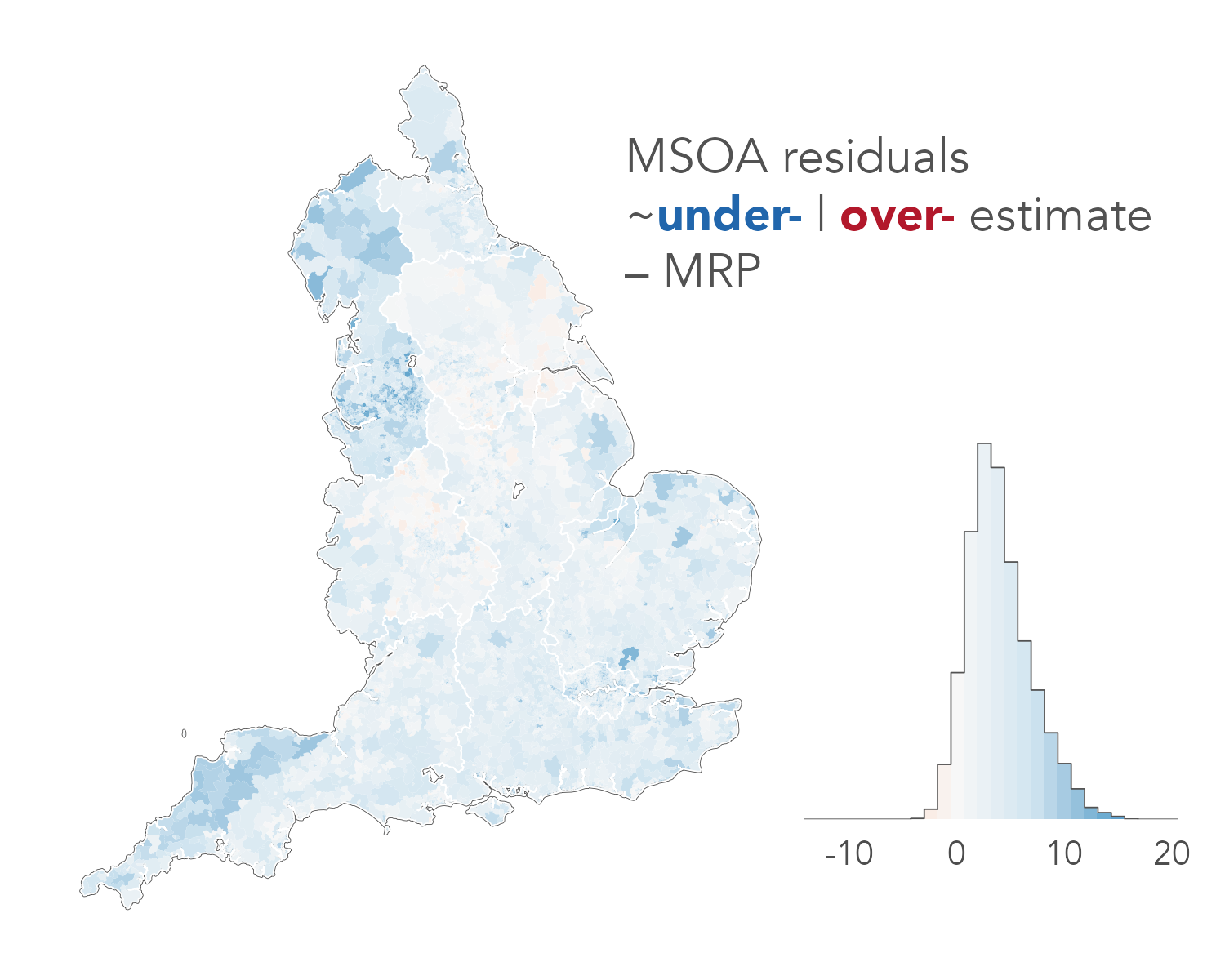
Comparison metrics

• Mean Absolute Error
  • # good | % good
• Pearson Residuals
  • obs-model / sqrt(model)
• Shannon Entropy
  • SPM only

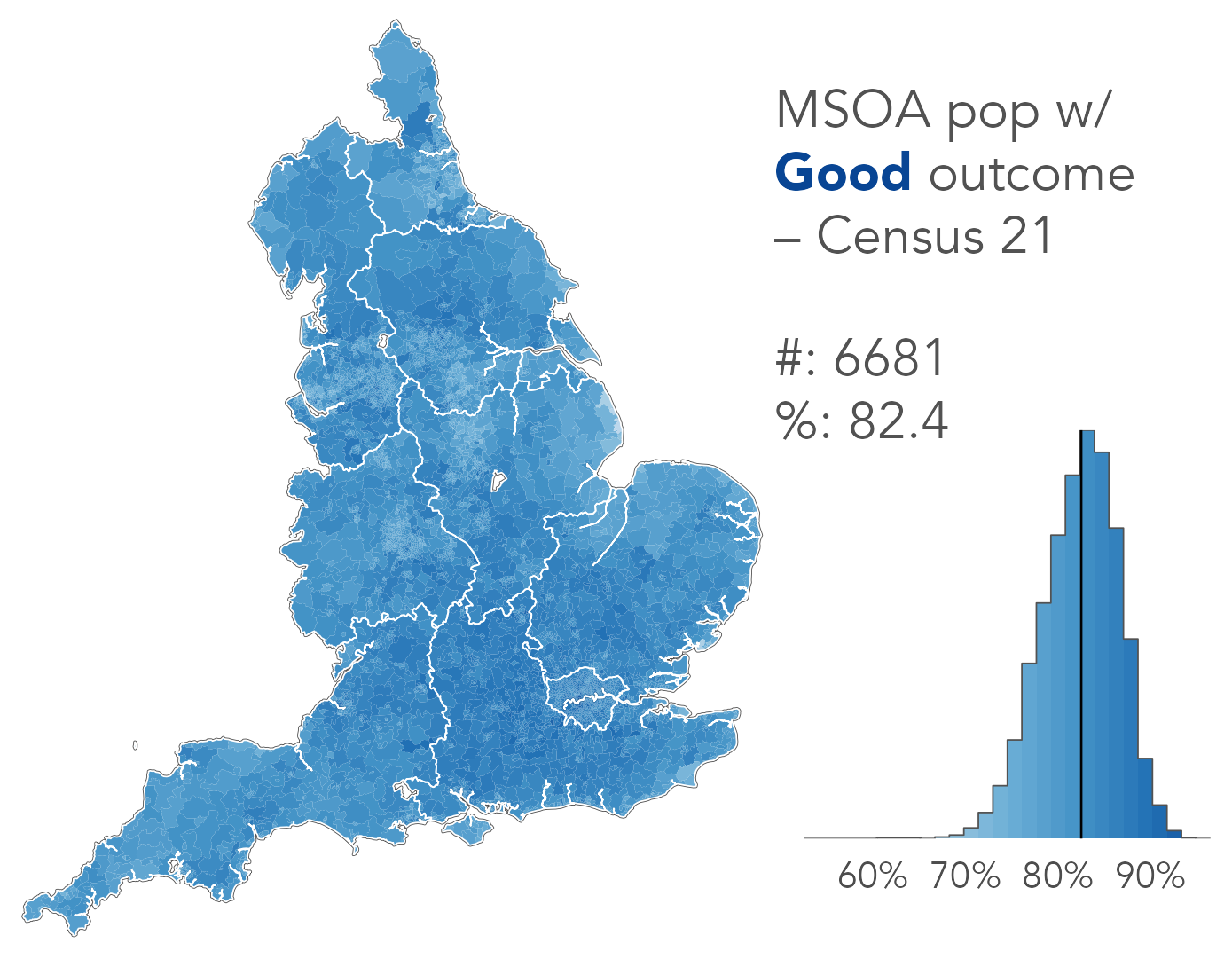
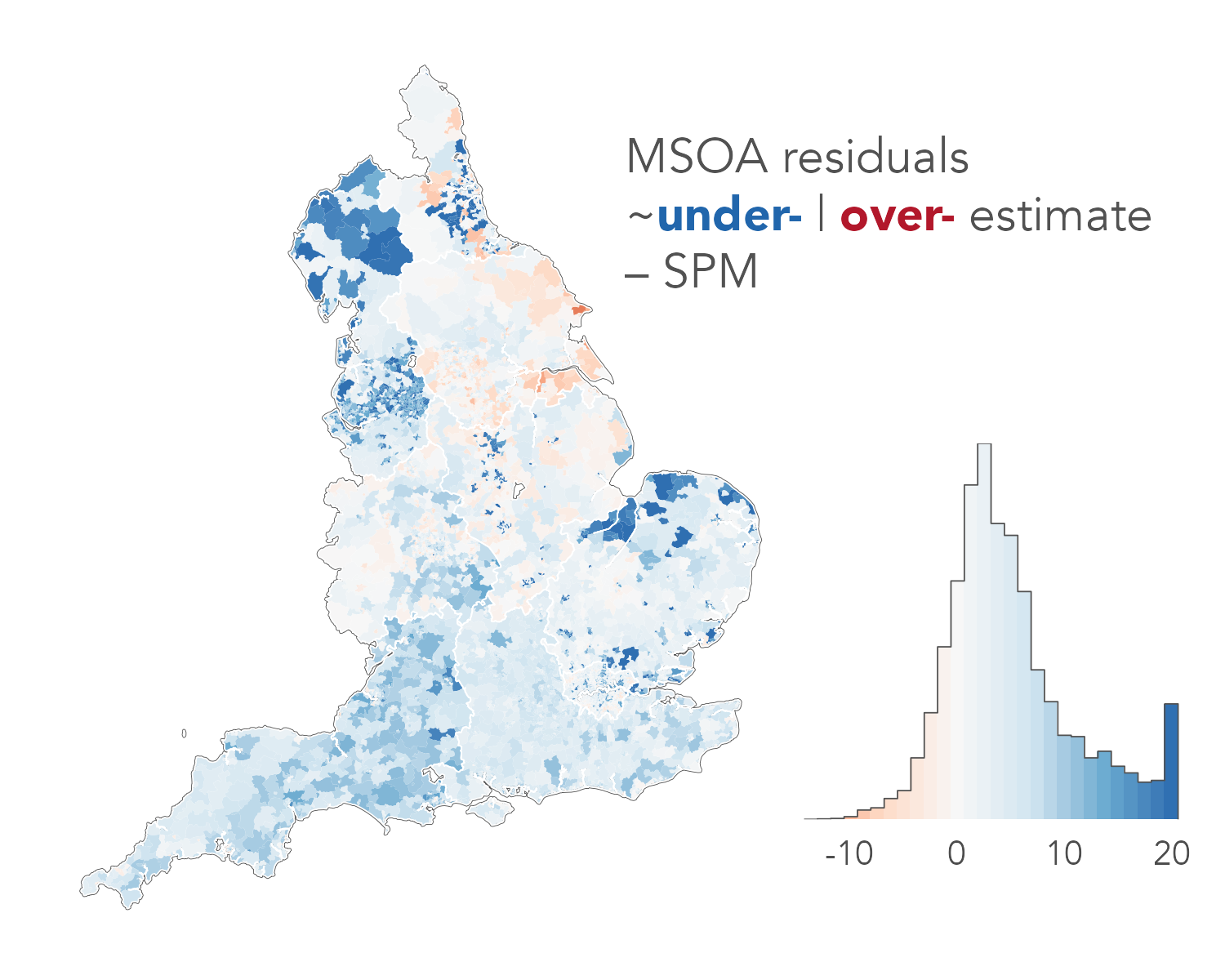
Results

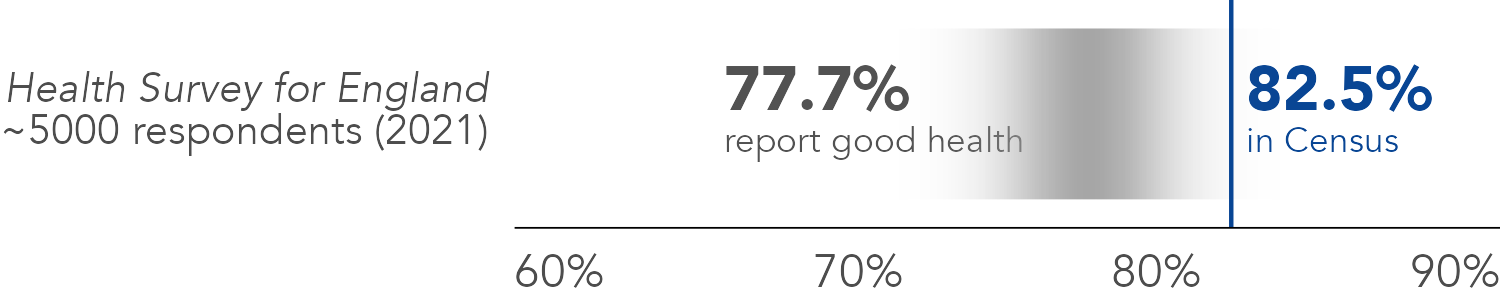
HSE underestimates
good outcome

Increasing model complexity

Increasing model complexity

Increasing model complexity

starts tp address some of misses that we were seeing in MRP

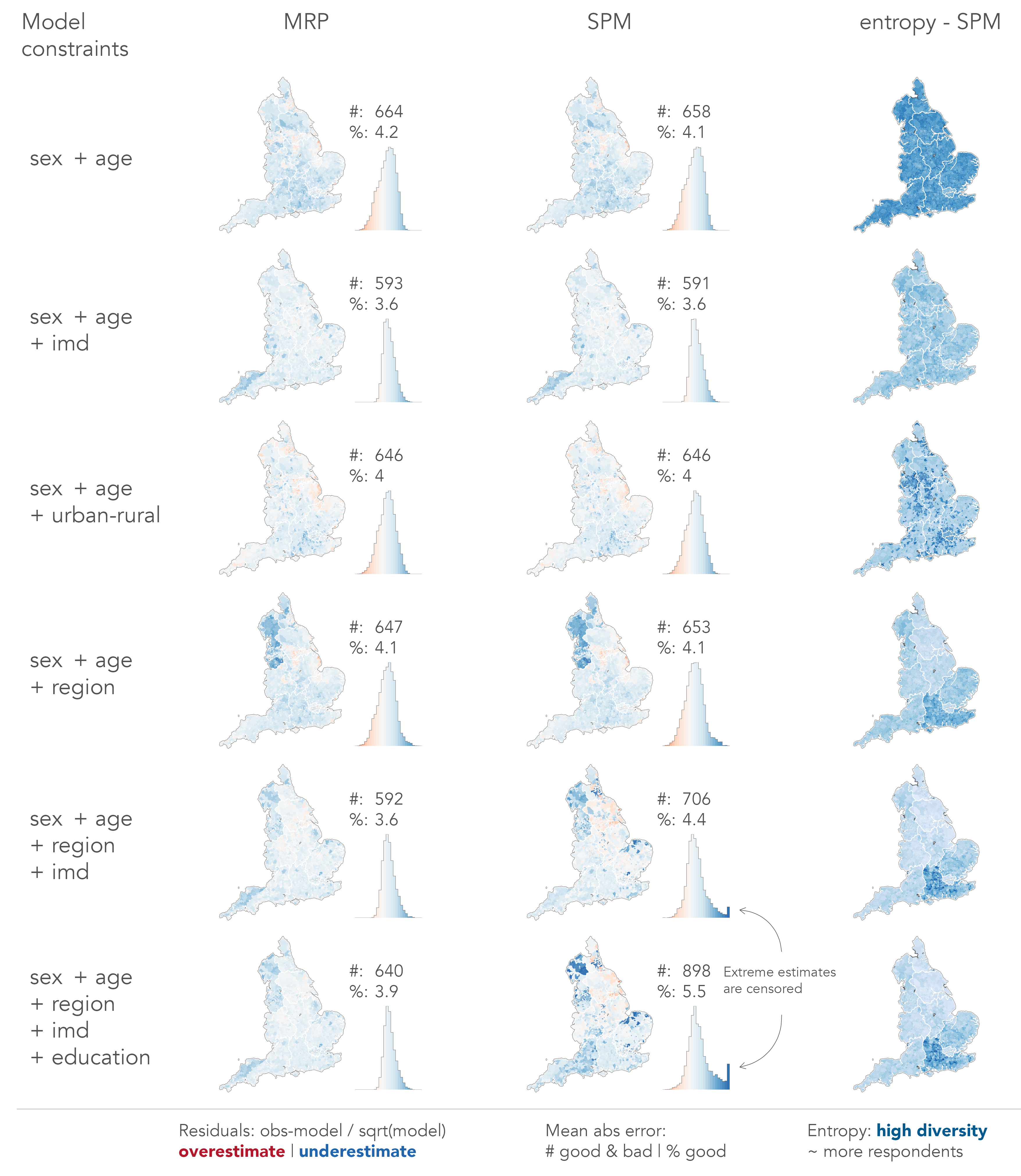
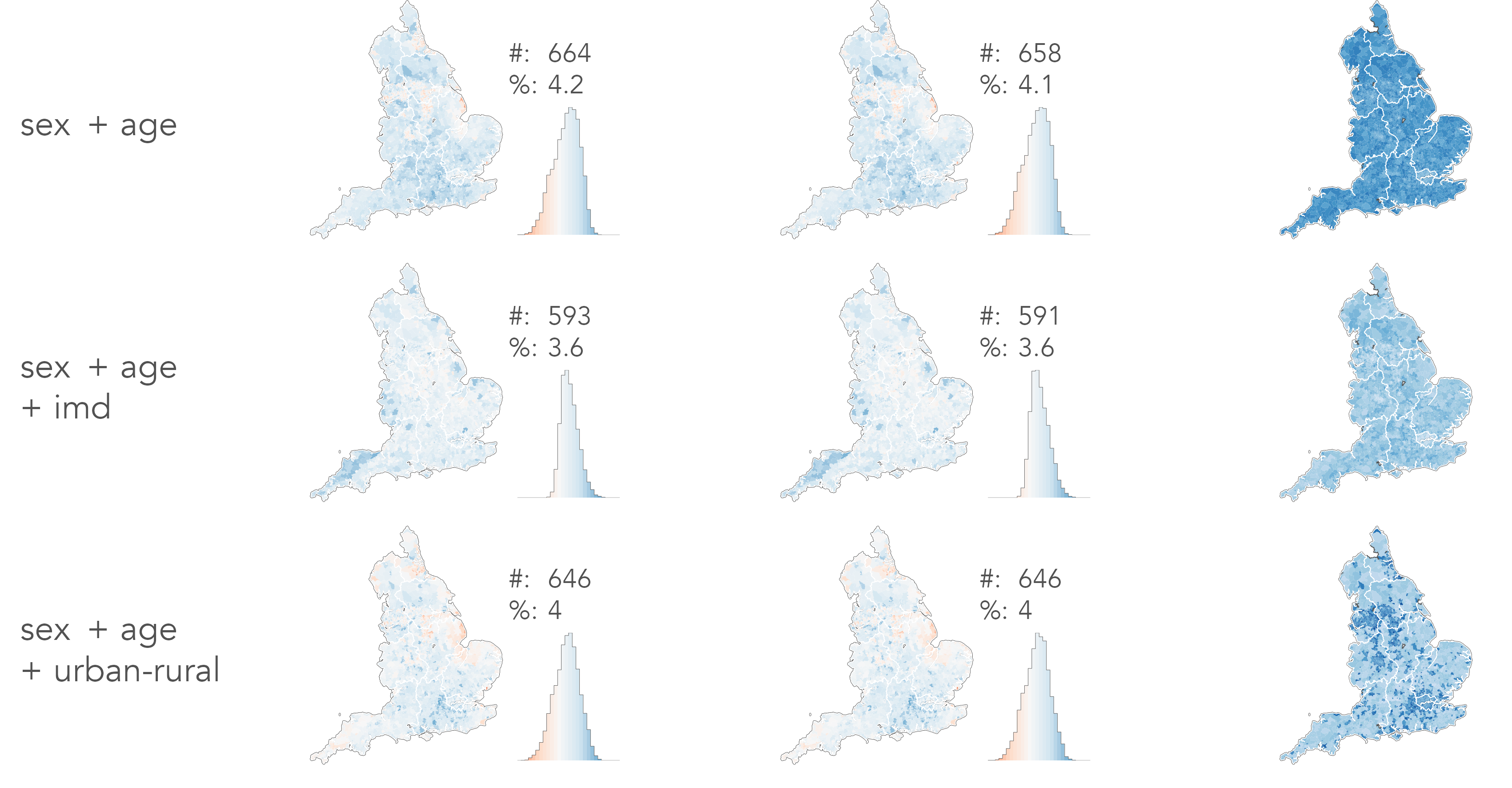
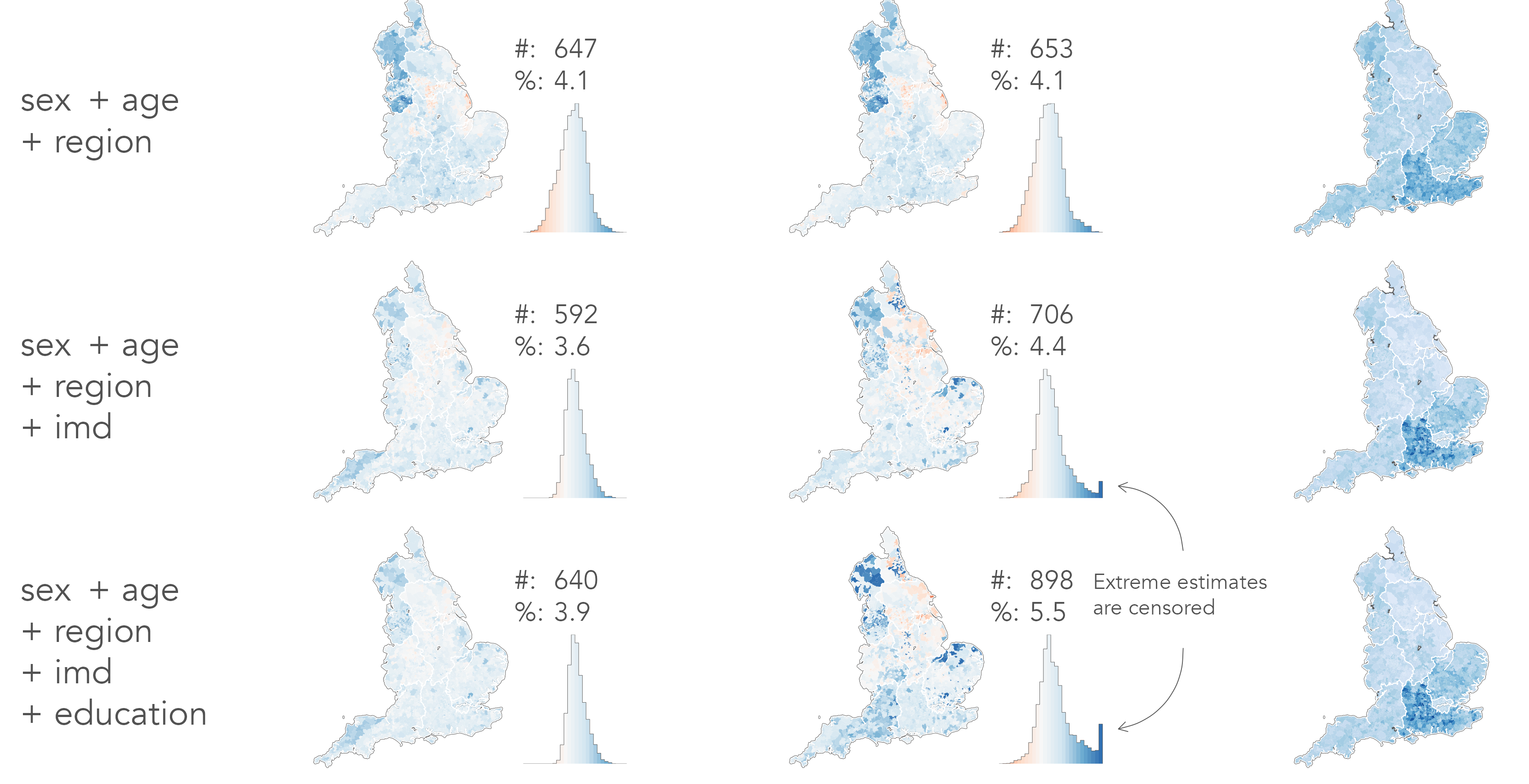
Discussion

Our thesis

1. Since it uses multilevel model designs – pooled estimates – MRP can estimate outcomes in small-areas poorly represented by survey data.

2. MRP adjusts for things that should bother us as geographers: modelled outcomes can reflect geographic dependency in outcome and heterogeneity in process.
   > Outcomes: {travel behaviour/ attitude, others}

3. MRP invites us to think in a principled way about the outcome and our inferences – as we explicitly model that outcome.

But that 1 is true, we have some evidence to support it: e.g. the way of dealing with this in SPM is to add hard geographic constraints and hope that the smaller number of individuals working from picks up that diversity in process… unlikely.

in the case of geog dependency in outcome – there are, thinking about travel behaviour area-level things that are going to bind that outcomethat are complex.

?

synthetic population
generation

github.com/rogerbeecham/…

–>

–>

–>

–>

–>

–>

–>

–>

–>

–>

–>

–>